A while ago a question Paul TOTH asked on Google+:
Please, could you add a “Use System debug DCU” with the “Uses debug DCU’s” checkbox to avoid the debuger to go in the low level System functions ?
During the comments I learned that Jeroen Wiert Pluimers asked a similar question on stackoverflow over a year ago. You can find some interesting approaches tackling that problem, but none of them looked clean and easy enough for me. So I tried to find another solution.
While solving the original problem (obviously) my solution should take care of the following constraints:
- Keep the Delphi installation untouched.
- Make it easy to work with.
- Adapt flexibly to different users needs.
- Easily switch back to the standard behavior (cause you never know).
Let’s start with some basics. The debug DCUs are located in the the lib folder of each (recent) Delphi installation, wherein you can find a folder for each supported platform. Inside these platform folders there is a release and a debug folder. The debug folder contains (you guessed it) the debug DCUs – the English ones. If you happen to have installed Delphi with at least one of the non English versions, you may find more folders for German (de), French (fr) and Japanese (ja).
The debug DCU folder is set in the Delphi options under Library / Debug DCU path. Usually you can find an entry like $(BDSLIB)\$(Platform)\debug there, which resolves to the correct path for each platform. There is another entry in Delphi options under Library – Translated / Translated Debug DCU path for the localized versions.
Now when you activate Use debug .dcus in the Debug configurations of your project options (it doesn’t make sense to activate it when you don’t want to debug), the IDE manages to insert the configured Debug DCU path into your search path before the Library path containing the release DCUs.
The drawback and the reason for the above mentioned questions is that you get either all debug DCUs in this folder or none at all. Wouldn’t it come handy when you can select which of those units you want in your debugging session and which not? This is where Selective Debugging steps in.
The mechanism is plain simple: Select the DCUs to debug and copy them in a separate folder. Then place this folder at the end of your projects Search path, which makes it appear before the Library path – just like the Use debug .dcus option does. The compiler searches for units in the entries of Search path first, then in those of Library path. This makes our selected files be found before those without debug information. Non selected DCUs are only found in the Library path.
As a consequence, when you enable the Use debug .dcus option in your build configuration you still end up with all debug DCUs just like before. Selective Debugging only works when this option is switched off.
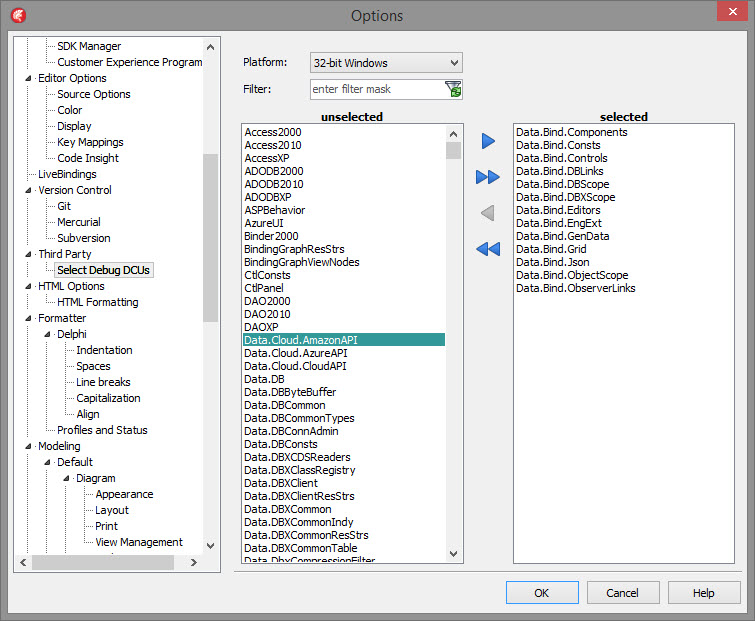
Selective Debugging is implemented as a Delphi design time package adding a new dialog named Select Debug DCUs to Tools – Options – Third Party. The dialog allows selecting individual units for debugging – for each platform separately. A filter allows to reduce the number of units displayed.
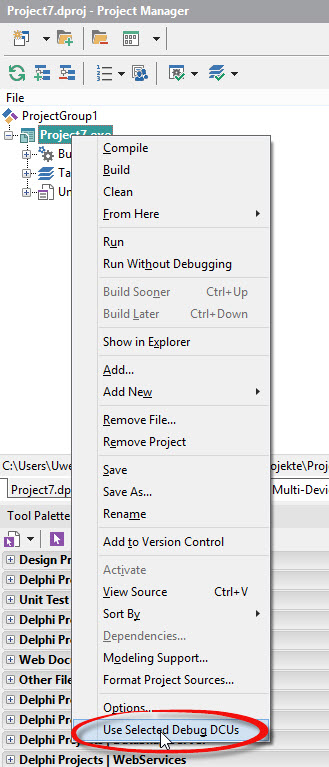
The package also adds a menu item to the Project Manager’s context menu when a project is selected (right at the bottom next to Options). Checking this menu item will add the Selective Debugging path to the projects search path, while unchecking will remove it (what else?).
The target folder for the selected debug DCUs is located in $(BDSCOMMONDIR) or $(BDSUSERDIR) depending on what you selected during the Delphi installation.
Update: The Selective Debugging package currently supports Delphi XE to Delphi 10.1 Berlin. It can be downloaded here: Selective Debugging

Isn’t this just the same approach as in my answer?
That’s the difference between theory (your SO answer) and practice (his useful plugin) 🙂
I just read the post as implying that Uwe was offering a different approach and I was curious to know what that would have been
The various solutions are generally all providing the compiler with a different order of search pathes combined with selectively distributed DCU files. If I correctly understand your proposal, it is merely the inversion of my solution, placing the release DCUs in a separate folder so they mask out the debug DCUs. Each way has advantages in different situations. One could have implemented your solution directly without changing the GUI of the plugin. I chose a slightly different approach for no specific reason besides it coming to my mind first. It has never been my intention to belittle your suggestion or that of others.
I’m pretty sure that your approach is the same as mine in essence. Looks like you did a good job.
Thanks a lot Uwe !
Interesting solution. My approach was much simpler:
A little script that changes NTFS junctions to the path I wanted to use for our own debug dcu files. So the junction path was contained in the normal library path, but pointed to either the dcu files with or without debug info.
The point of the plugin is to control which files to step into. And not only to switch between debug/no debug.